§5.2
定积分的性质、中值定理
规定:
1、![]() 时,
时,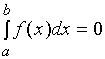
2、![]() 时,
时,
这两条规定的意义较直观。
当![]() 时,曲边梯形退缩成一段线, 故其面积
时,曲边梯形退缩成一段线, 故其面积 应该为零;
应该为零;
当![]() 时,区间
时,区间![]() 所对应的分点成为
所对应的分点成为
![]()
相应的小区间的长度
![]() 。
。
此时,相对于 ,
,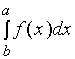 的符号应相反。
的符号应相反。
声明:在下面的讨论中, 对积分上下限的大小均不加以限制,并假定各性质中所列出的定积分均存在。
【性质一】函数的和(差)的定积分等于它们的定积分的和(差)。
即: 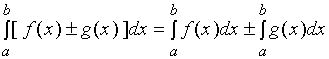
证明:

显然,性质一对于任意有限个函数也是成立的。
【性质二】被积函数的常数因子可以提到积分号外面。
即:![]() (
( ![]() 是常数因子 )
是常数因子 )
证明:
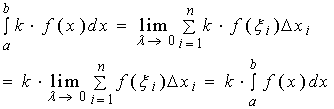
【性质三】如果将积分区间分成两部分,
则在整个区间上定积分等于这两个区间上定积分之和。
即: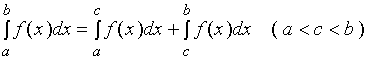 ( * )
( * )
这一性质的几何意义十分明显。如图,曲边梯形的面积有:

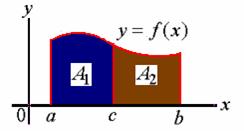
此性质表明,定积分对于积分区间具有可加性。其实,无论三个数![]() 的相对位置如何,等式( * )总是成立的。
的相对位置如何,等式( * )总是成立的。
例如:当![]() 时, 有
时, 有
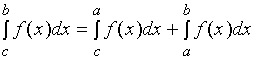

【性质四】如果在区间![]() 上,
上,![]() ,则
,则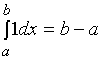 。
。

【性质五】如果在区间![]() 上,
上,![]() ,则
,则 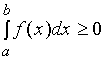 。
。
据定积分几何意义,它是一个曲边梯形真正的面积值,故它应为非负的。
【推论一】如果在区间![]() 上,
上,![]() ,则
,则
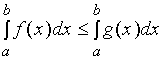
事实上,
由 ![]() , 据 性质五 与 性质一 有
, 据 性质五 与 性质一 有

【推论二】
证明:![]()
由推论一有:
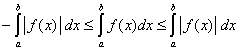
即: 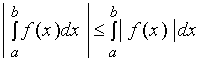
【性质六】设![]() 及
及![]() 分别是函数
分别是函数![]() 在区间
在区间![]() 上的最大值及最小值,
上的最大值及最小值,
则 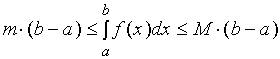
证明:![]()
则 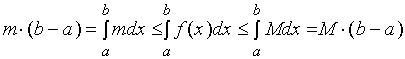
这一性质可用来估计定积分值的范围,它也具有鲜明的几何意义。
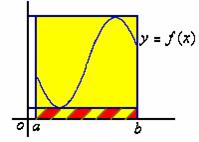
【性质七】( 定积分的中值定理 )
如果函数![]() 在闭区间
在闭区间![]() 上连续, 则在
上连续, 则在![]() 上至少存在一点
上至少存在一点![]() ,
,
使得 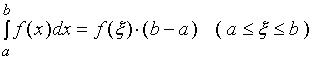
证明:据性质六有
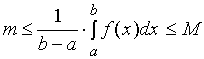
数值 介于连续函数
介于连续函数![]() 在
在![]() 上的最小值
上的最小值![]() 与最大值
与最大值![]() 之间, 再由闭区间上连续函数的介值定理, 在
之间, 再由闭区间上连续函数的介值定理, 在 ![]() 上至少存在一点
上至少存在一点 ![]() ,使得
,使得
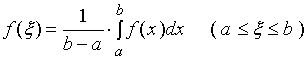 。
。
积分中值公式的几何解释

利用计算机编写程序gs0502.m,对定积分
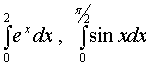
进行数值计算试验,我们可验证定积分中值定理的正确性。运行该程序时,注意建立被积函数的函数文件f.m